 Overview of GNODE.
Overview of GNODE.Abstract
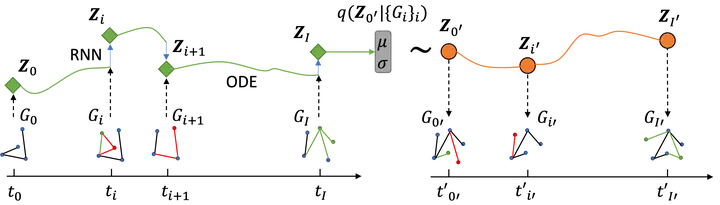
Dynamic graph forecasting has found a wide range of applications including social media, recommendation systems, and computational finance. However, existing dynamic graph models typically focus on discrete-time dynamic graphs, treating dynamic graphs as temporally discrete graph snapshots. We argue that such discrete treatment is inadequate for capturing the underlying dynamics which are intrinsically continuous. To overcome such deficiency, we extend fully connected neural ordinary differential equations (FCNODE) to graph-connected neural ordinary differential equations (GNODE), which considers graph structures in the input space, output space, and the transition in the latent space. Experiments show that our GNODE naturally captures the continuous-time dynamics in graph sequences and consistently outperforms state-of-the-art graph forecasting methods.